MATEMATICAS 2 PERIODO
SEMANA 11
SEMANA 11 abril 12 al 16
PPLANO CARTESIANO y PAREJAS ORDENADAS (Trabajo 2 Horas)
Cuando relacionamos dos conjuntos, podemos armar parejas como ( 3 , 9 ) y ubicar estas parejas en un plano llamado cartesiano, donde hay coordenadas X en las horizontales y coordenadas Y en la verticales, y cada cuadro se denomina un cuadrante, así.
s El primer número se ubica en el eje X y el segundo número en el eje Y.
ejemplo: ( 2 , 3 ) y se ubica la pareja donde se encuentren los dos puntos.
Cuando los números están debajo de la línea horizontal y al lado izquierdo, se escriben con un signo menos y serán números negativos ( - 3 , - 1 )
ACTIVIDAD
Ubique las parejas con un punto, una los puntos y descubra el dibujo.
Miguel Ángel pintó la Capilla Sixtina en el siglo XVI
Para nombrar a los reyes: Fernando II de Aragón se casó con Isabel I de Castilla
Para numerar los tomos o partes de algunos libros o películas: Ayer vi en la televisión El padrino I
Para aniversarios, reuniones o festejos que se celebran periódicamente: Se está organizando el IV certamen de fotografía juvenil
NÚMEROS ROMANOS
LA MULTIPLICACIÓN
Multiplicación es una suma abreviada, donde se suma un número tantas veces como lo indique el otro por ejemplo: 45 X 3 = 45 + 45 + 45 =135
Términos de la multiplicación
estas son términos de la multiplicación.
ACTIVIDAD
Realizar las siguientes multiplicaciones
2. Mandar un video de un minuto máximo, diciendo de forma rápida y con los ojos cerrados y de memoria las tablas del 9 y del 8. (Actividad que se había anunciado repasar desde el primer periodo.)
PROPIEDADES DE LA MULTIPLICACIÓN
Estas son las propiedades: conmutativa, asociativa, modulativa, distributiva y clausurativa.
Propiedad distributiva: La suma de dos números multiplicada por un tercer número es igual a la suma de cada sumando multiplicado por el tercer número.
Por ejemplo 4 x (6+3) = 4 x 6 + 4 x 3
- Propiedad conmutativa
El orden de los factores no altera el producto. Si se multiplican dos números, el producto es el mismo sin importar el orden Por ejemplo: 4 x 2 = 2 x 4
Propiedad asociativa
Cuando se multiplican tres o más números, el producto es el mismo sin importar como se agrupan los factores.Por ejemplo (2 x 3) x 4 = 2 x (3 x 4)
Propiedad modulativa
El producto de cualquier número natural por el número 1, el producto es el mismo. da como resultado el mismo número. Para la multiplicación, el módulo es el número 1.
Al realizar una operación con números naturales siempre nos da es un número natural.
ACTIVIDAD
1. Completa. utilizando la propiedad distributiva.
4 x (2 + 5) = ( x -) + ( x ) =
8 x (10 + 7) = ( x ) + ( x ) .=
2.
https://www.youtube.com/watch?time_continue=109&v=c11n-QDzTGk&feature=emb_logo
Múltiplos de un número.
Los múltiplos de un número son aquellos que se obtienen al multiplicar un numero por otro.
Para saber si un número es múltiplo de otro, se divide y el cociente es el múltiplo si el residuo de la división es 0.
Un múltiplo común es aquel que es múltiplo a la vez de dos o más números.
ejemplo:
Para hallar el mínimo común múltiplo de dos o más números debemos de descomponer el número en factores primos.
Por ejemplo: Descomponer 40 y 60 en sus factores primos
Por lo tanto 60 se descompone en: 2x2x3x5
El mínimo común múltiplo (mcm) es el número más pequeño que es múltiplo de dos o más números.
Vamos a calcular el mínimo común múltiplo de 4 y 6. Para ello, escribimos los primeros múltiplos de 4 y de 6:
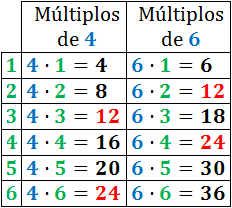
Entre los múltiplos de 4 y de 6, el número 12 es el múltiplo común mas pequeño entre ambos números.
Por tanto, el mínimo común múltiplo se escribe de la siguiente manera:
![]()
Divisores de un número.
https://edu.gcfglobal.org/es/divisores-y-multiplos/
Los divisores de un número son
aquellos que pueden dividir a otro y el residuo es cero.
Para saber si un número es divisor de
otro, solo tienes que hacer la división y comprobar si el resto es cero.
Ejemplo
¿Cuáles son los divisores de 15? Son números entre los que podemos dividir el 15 siendo el residuo 0. Luego los divisores del 15 son el 1, el 3, el 5 y el 15.
Criterios de divisibilidad.
Podemos saber
fácilmente si un número es divisible por otro sin hacer la división,
simplemente observando estas características:
- Los múltiplos de 2 terminan en 0, 2, 4, 6, 8.
- Es múltiplo de 3 si al sumar sus cifras dan como resultado un múltiplo de 3.
s· - Un número es divisible entre 4 si el número formado por las dos últimas cifras es un múltiplo de 4 o cuando termina en doble cero.
- Los múltiplos de 5 terminan en 0 o en 5.MAXIMO COMUN DIVISOR
Para determinar el MCD podemos determinar cuales números dividen de forma exacta cada número dado, luego miramos cual es el máximo número que se repite en ambos números.
Ejemplo calculemos los divisores de y :
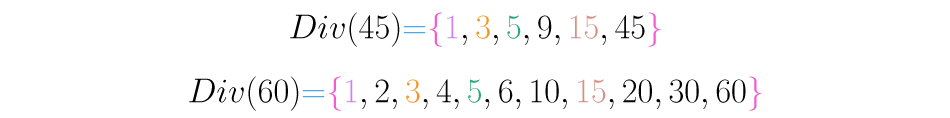
Observa que los números y son divisores comunes de y . El mayor de estos números, es el máximo común divisor.
Para el caso de y , se tiene que el máximo común divisor es .
https://www.youtube.com/watch?v=6Z16NW7s1Iw&t=17s
Un procedimiento más sencillo y corto para calcular el máximo común divisor de y es descomponerlos en factores primos.
Primero se debe realizar la descomposición de cada uno de los números hasta donde se pueda dividir ambos números:
21 36
81 10 45
25 y 22
44 88
Los polígonos
Partes del polígono
Lados: son los segmentos
que forman la línea poligonal.
Vértices: son los puntos
donde se unen los lados.
Ángulos: son las regiones
del plano que delimitan dos lados.
Diagonal: es la recta que une
dos vértices no consecutivos.
Centro: es el punto desde
el que todos los ángulos y lados están a la misma distancia.
Radio: es el segmento que
une el centro del polígono con cualquiera de sus vértices
Apotema: es el segmento que
une el centro del polígono con el centro de cualquiera de sus lados.
Base: Es el lado inferior de un polígono. Normalmente es el lado donde se “apoya” la figura.
Clasificación de polígonos
· Clasificación de polígonos según sus lados:
o
o
Cuadrilátero: 4 lados
o
Pentágono: 5 lados
o
Hexágono: 6 lados
o
Heptágono: 7 lados
o
Octógono: 8 lados
o
Eneágono: 9 lados
o
Decágono: 10 lados
o
Endecágono: 11 lados
o
Dodecágono: 12 lados
Clasificación
de polígonos según sus lados y sus ángulos:
Polígonos regulares: es cuando un polígono tiene todos sus lados y
ángulos iguales.
Polígonos irregulares: es cuando en un polígono hay uno o más lados y/o
ángulos que no son iguales.
ACTIVIDAD
El perímetro de un polígono es igual a la suma de las longitudes de sus lados y su área es la medida de la región o superficie encerrada por un polígono.
ACTIVIDAD
Calcular el área y el perímetro del siguiente trapecio:
Calcular el área del siguiente polígono:
Hallar el área de un triángulo rectángulo cuyos lados miden
Ejemplo tenemos los siguientes datos
Primero reordena los datos del más pequeño al más grande.
por esto La mediana es 89.
Encontraremos la moda.
La moda es el número que aparece más veces. En este caso, 85 aparece dos veces y todos los otros números aparecen solo una vez. El número 85 es la moda.
La moda es 85.
El rango es la diferencia entre el valor más alto y el valor más bajo en un conjunto de datos.
62 dato mas pequeño menos 105 dato mas grande
105-62= 43 este es el rango.
Práctica Guiada
Aquí hay un ejercicio para que trates tú mismo.
Encuentra la media, mediana, moda y rango del siguiente conjunto de datos.
Solución
Primero, encontramos la media al sumar todos los valores en el conjunto de datos y luego dividimos por el número de valores en el conjunto.
La media es .
La media es el punto medio. Ya que los valores ya están en orden de menor a mayor, simplemente podemos encontrar el valor medio.
La mediana es .
No hay moda.
Para encontrar el rango, encontramos la diferencia entre el valor más alto y el valor más bajo.
El rango es .
https://flexbooks.ck12.org/cbook/ck-12-conceptos-de-matem%c3%a1ticas-de-la-escuela-secundaria-grado-8-en-espa%c3%b1ol/section/10.1/primary/lesson/media-mediana-moda-y-rango






































Comentarios
Publicar un comentario